Nc
Degré de liberté
Désignation et définition
Schématisation
Torseur cinématique
Repère idéal
plane
perspective
O
![]()
1
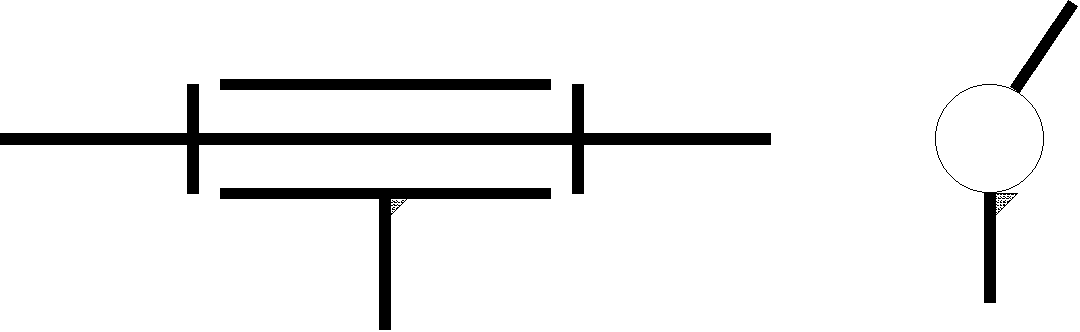

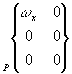
![]()
1

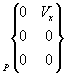
![]()
1

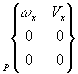
![]()
![]()
2
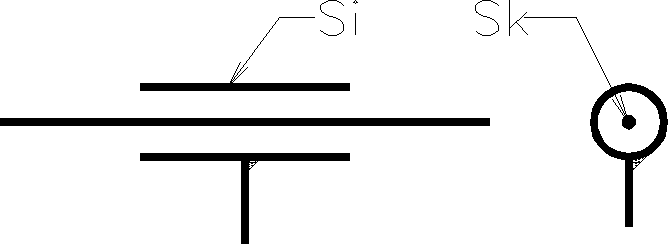
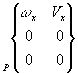
![]()
2
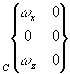
3
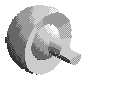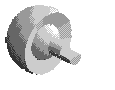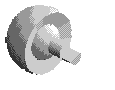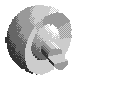
3
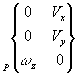
![]()
4
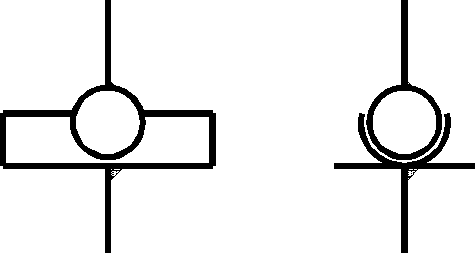
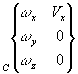
C centre de la sphère.
4
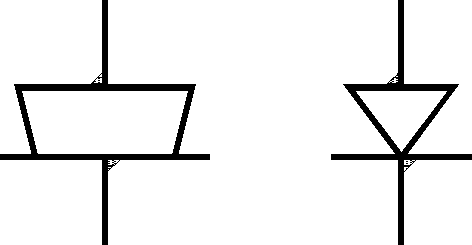
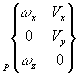
L'axe x est porté par la droite de contact
![]()
5
![]()
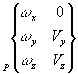
![]()
LIAISONS ENTRE SOLIDES . Liaisons entre solides.

1. Liaisons normalisées entre solides.
a) Schémas normalisés
2. Degrés de liberté d'un solide par rapport à un autre:
3. Paramétrage géométrique de la position d'un solide par rapport à un autre.
a)Tableau des liaisons normalisées
Modélisation cinématique et géométrique des liaisons
Nous avons vu que la position d'un solide dans l'espace peut être définie par 6 paramètres, 3 Rotations et 3 Translations.
Ces 6 paramètres sont les 6 degrés de libertés du solide.
En fait un solide n'est généralement pas seul, il est en liaison avec d'autres solides. Cette liaison va limiter le nombre de degrés de liberté existant entre les solides.
L'étude des liaisons réelles existantes entre les différentes pièces d'un mécanisme est délicate et difficile en effet, les défauts entre les surfaces de contact (rugosité, défaut de forme), la présence de jeu, la déformation des pièces, les frottements, et l'usure.
Afin de pouvoir étudier le fonctionnement d'un mécanisme, il est nécessaire de modéliser les liaisons entre les différentes pièces.
Une liaison est dite parfaite si:
- Le contact s'établit théoriquement en un point, sur une ligne ou sur une
surface de définition géométrique simple (plan sphère, cylindre, surface hélicoïdale,
..);
- Les surfaces de contact sont supposées géométriquement parfaites;
- la liaison est sans jeu.
La norme NF E04-015 présente les onze liaisons élémentaires.
. (Voir tableau)
Degrés de liberté d'un solide par rapport à un autre:
On appelle degré de liberté d'un solide par rapport à un autre le nombre de mouvements élémentaires indépendants (3 rotations et 3 translations) entre les deux solides. Le nombre de degré de liberté de chaque liaison élémentaire est indiqué dans le tableau récapitulatif.
Paramétrage géométrique de la position d'un solide par rapport à un autre.
|
Nc |
Désignation et définition |
Schématisation |
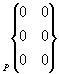
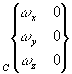
Torseur cinématique |
Repère idéal |
||
|
plane |
perspective |
Animation | ||||
|
O |
Liaison encastrement ou liaison fixe |
|
|
 |
||
|
1 |
Liaison Pivot |
|
|
 |
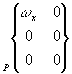 |
L'axe
x du repère idéal passe par l'axe de la liaison pivot.
|
|
1 |
Liaison Glissière: |
|
|
 |
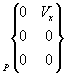 |
axe
x du repère idéal passe par l'axe de la liaison glissière
|
|
1 |
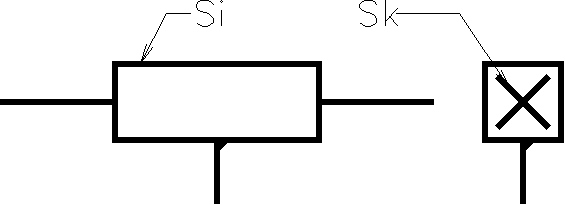
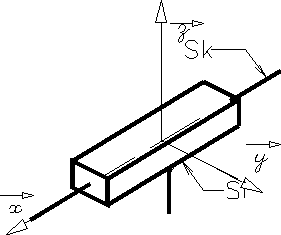
Liaison hélicoïdale |
|
|
 |
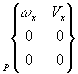 |
Idem
|
|
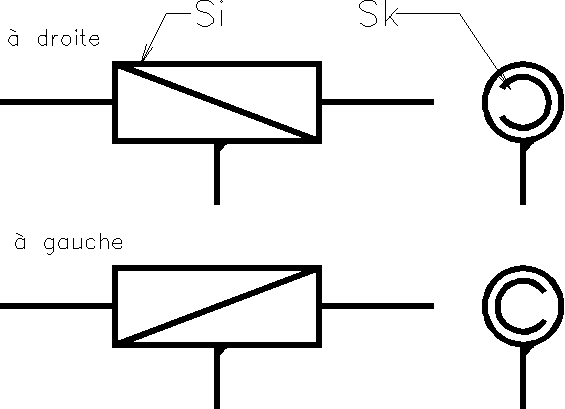
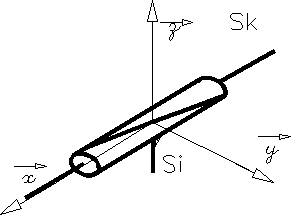
2 |
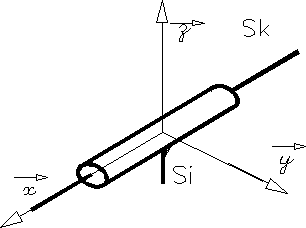
Liaison Pivot Glissant |
|
|
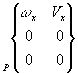 |
L'axe
x du repère idéal passe par l'axe de la liaison pivot glissant.
|
|
|
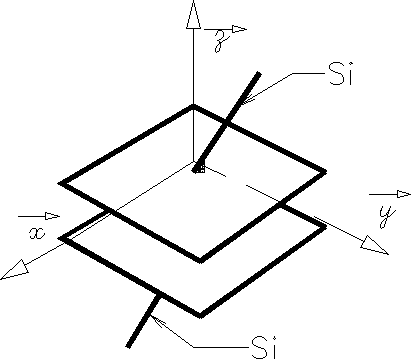
2 |
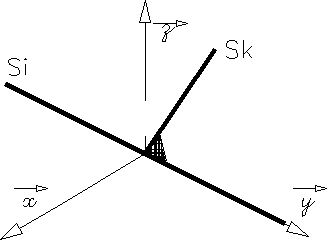
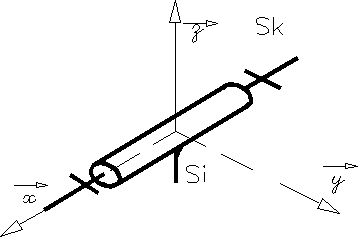
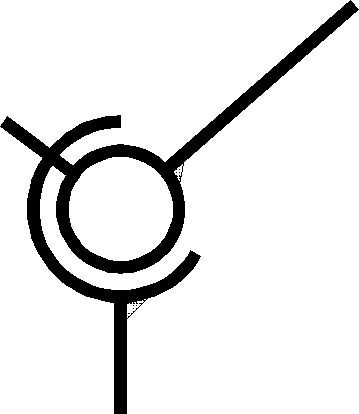
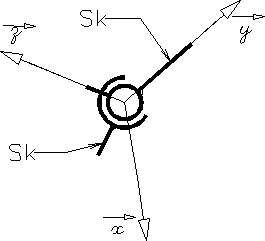
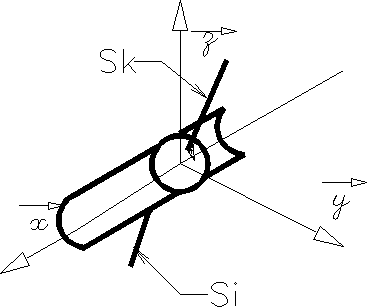
liaison Sphérique à doigt |
|
|
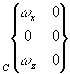 |
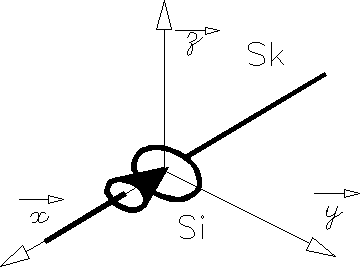
L'axe z du repère idéal passe par l'axe du doigt, l'axe x est perpendiculaire au plan de la rainure. Le point de réduction du torseur cinématique est le point O centre de la sphère. | |
|
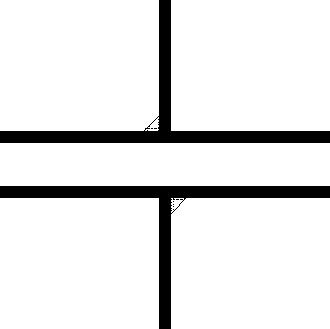
3 |
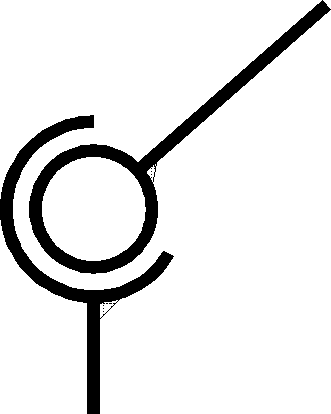
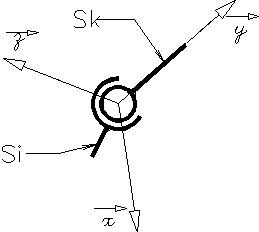
liaison Rotule ou Sphérique |
|
|
 |
 |
Le point de réduction du torseur cinématique est le point C centre de la sphère. Le repère idéal passe par ce point |
|
3 |
liaison Appui Plan |
|
|
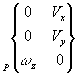 |
L'axe
z est perpendiculaire au plan
|
|
|
4 |
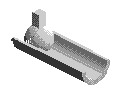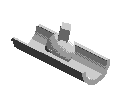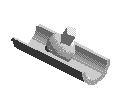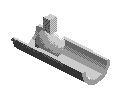
liaison Linéaire Annulaire |
|
|
 |
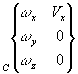 |
l'axe
x est l'axe du cylindre.
C centre de la sphère. |
|
4 |
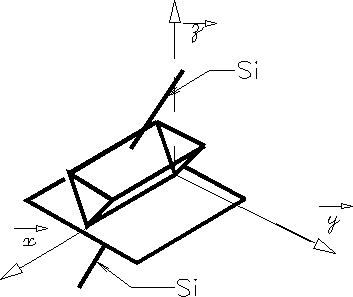
Liaison Linéaire Rectiligne |
|
|
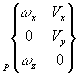 |
Axe
z normale au plan tangent.
L'axe x est porté par la droite de contact
|
|
|
5 |
Liaison Ponctuelle |
|
|
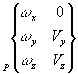 |
Axe
x normale au plan tangent.
|
|
Envoyez un courrier électronique à qaidi@caramail.com pour toute question ou remarque concernant ce site Web.
Dernière modification : 21 février 2001